This is a complex number: $$z = x + iy$$
A complex number, as a combination of a real number ($x$) and an imagenary number ($iy$, or $yi$, it doesn’t matter) can be sketched with 2-dimentional axis. Note that $y$ is a real number, and $i$ is an imagenary number ($i = \sqrt{-1}$).
This is an example from mathbits :
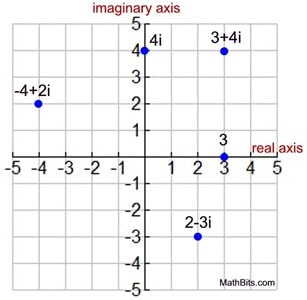
The real axis represents the real number $x$, with each unit representing 1. The imagenary axis represents the imagenary part $iy$, each unit representing $i$, and $y$ represents the number of units.
Also, to represent an complex number with number pairs, we can use the format of $(x, y)$. For example, $i=2+3i$ can be noted down as $(2,3)$.
If you have learned Calc 2, you may have heard about polar coordinates. We can also use polar system to sketch complex numbers.
For example, $z=x+iy$ can be represented as:
$$z= r(\cos{\theta}+i\sin{\theta})$$
Here is an image copied from Online Math Learning Website
:

To use pairs, we can note down in $(r, \theta)$ form. For example, $z=1+i$ can be represented as $(\sqrt{2}, \frac{\pi}{4})$ (45 degree angle), or to be more cautious let’s write down $(\sqrt{2},\frac{\pi}{4}+2k\pi)$, if you rotate extra 360 degrees, 720 degrees, etc. You are back to where 45 degree line locates.
If you have learned Calc 2, you may also have heard of Taylor Series. You can use Taylor Series to get a wierd form: $$\cos{\theta}+i\sin{\theta}=e^{i\theta}$$
Here is a proof from YouTube:
Then, the complex number $z=x+iy$ can be represented as:
$$z=r(\cos{\theta}+i\sin{\theta})=re^{i\theta}$$
When you have the $e$ form of the complex number, if you would like to calculate the root or power of it, it’s becoming simpler.
Hmm, why do I care about this? Well, if someone ask you to calculate the root of complex numbers, the power of complex numbers, the mod of complex number, all the process gets easier.
For example, how to calculate $\left|\left(\frac{1+i}{1-i}\right)^5\right|$? I mean the mode, or the length of $\left(\frac{1+i}{1-i}\right)^5$.
You can calculate the power first, or you can calculate the faction, but I am too lazy to do that. What about using the magical $re^{i\theta}$?
$$ \left|\left(\frac{1+i}{1-i}\right)^5\right| = \left|\left(\frac{\sqrt{2}e^{i(\frac{\pi}{4})}}{\sqrt{2}e^{i(-\frac{\pi}{4})}}\right)^5\right| = \left|\left(e^{i\frac{\pi}{2}}\right)^5\right| = \left|e^{i\frac{5\pi}{2}}\right| = 1$$
Apologize: I am too lazy to type out the case of $2k\pi$ and draw the curve.
Last modified on 2024-02-03